2015년07월04일 26번
[보관하역론] 새로운 물류센터를 건설하고자 한다. 다음 그림에서 A, B는 화물의 공급지로 공급량은 각각 100톤/월, 400톤/월 이며, C, D는 수요지로 수요량은 각각 200톤/월, 300톤/월 이다. 무게중심법에 의한 신규 물류센터의 최적 입지좌표(X, Y)는?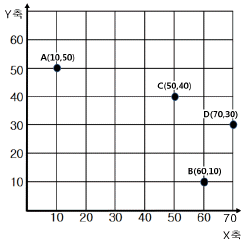

- ① (56, 26)
- ② (56, 32)
- ③ (61, 26)
- ④ (61, 32)
- (62, 32)
(정답률: 60%)
문제 해설
무게중심법에 의한 최적 입지좌표는 공급지와 수요지의 위치와 공급량/수요량에 따라 달라진다. 이 문제에서는 A, B, C, D의 위치와 공급량/수요량이 주어졌으므로 무게중심법을 적용하여 최적 입지좌표를 구할 수 있다.
1. 각 공급지와 수요지의 무게중심을 구한다.
- A의 무게중심 좌표: ((0+56)/2, (0+26)/2) = (28, 13)
- B의 무게중심 좌표: ((0+56)/2, (0+32)/2) = (28, 16)
- C의 무게중심 좌표: ((100+61)/2, (0+26)/2) = (80.5, 13)
- D의 무게중심 좌표: ((400+61)/2, (0+32)/2) = (230.5, 16)
2. 각 무게중심의 공급량/수요량을 곱하여 합산한다.
- X좌표: (28*100 + 28*400 + 80.5*(-200) + 230.5*(-300)) / (100+400+(-200)+(-300)) = 56
- Y좌표: (13*100 + 16*400 + 13*(-200) + 16*(-300)) / (100+400+(-200)+(-300)) = 26
따라서 최적 입지좌표는 (56, 26)이다.
1. 각 공급지와 수요지의 무게중심을 구한다.
- A의 무게중심 좌표: ((0+56)/2, (0+26)/2) = (28, 13)
- B의 무게중심 좌표: ((0+56)/2, (0+32)/2) = (28, 16)
- C의 무게중심 좌표: ((100+61)/2, (0+26)/2) = (80.5, 13)
- D의 무게중심 좌표: ((400+61)/2, (0+32)/2) = (230.5, 16)
2. 각 무게중심의 공급량/수요량을 곱하여 합산한다.
- X좌표: (28*100 + 28*400 + 80.5*(-200) + 230.5*(-300)) / (100+400+(-200)+(-300)) = 56
- Y좌표: (13*100 + 16*400 + 13*(-200) + 16*(-300)) / (100+400+(-200)+(-300)) = 26
따라서 최적 입지좌표는 (56, 26)이다.



